The Value of Life

Why would you pay more for engineering than for the ship? The value of engineering comes from the lives protected, not the design of the yacht. How much is that protection worth? This risk analysis has an answer to the value of safety.

Engineering Risk Analysis

1.0 Introduction

Here is a riddle that puzzled me for a long time:  why would you pay for an engineer to design a small yacht when the engineering costs more than the yacht?  As a consultant engineer, I often consider the value of my services.  I search for opportunities where the benefit of engineering matches the cost.  And small boats always defied logic for me.  For small ships and yachts, the cost of the engineering often exceeds the value of the ship.

Why would you pay more for engineering than for the ship?  I pondered this for several years.  That seems easy to justify on a production yacht:  design it once and build multiple copies.  But it still takes several sales to recoup the cost of engineering.  Is engineering even justified for small ships? 

Then I realized the value of the engineer was not in the yacht it produced.  The value lied in the lives that yacht protects.  The primary value of an engineer is not to produce a pretty yacht.  We produce a SAFE ship.  A product that protects human life.  But I always think about the business implications, so I have to ask:  how much is that protection worth?

2.0 What is Safe

The answer to that question comes from risk analysis.  This is a general field focused on predicting the value of safety.  Risk analysis allows us to quantify scary things and decide on an appropriate level of safety.  It also ensures we don’t go overboard with safety.  Today, I demonstrate the power of risk analysis by looking at the value of engineering on yachts.

The mathematics behind risk analysis get very intense when we consider complicated systems like a nuclear reactor.  But the core concept behind all that math is simple.  “Risk” is the probability that something bad happens, multiplied by the consequences of that event.  Answer two questions:  what are the odds of something happening?  And what is the outcome of that event?  Then you know the risk.

Insurance companies love risk analysis.  It gives them a basis to set the premiums for insurance, because they can quantify the average payout for all the accidents in a year.  And much of that payout centers around the cost in human lives.  Which means that they absolutely place a value on human life.

3.0 The Value of Human Life

$10 million dollars.  That is the approximate value of a single human life.  At first, I thought this was too high.  But I found two sources that roughly agreed with this number.  The first source came from a statistical comparison of hazard pay people will accept to work higher risk jobs. [1]  I couldn’t believe it at first.  So, I also checked on lawsuits.  Wrongful death lawsuits are the real fear for a manufacturer.  The results varied wildly, but one law firm posted results from some of their cases.  The payouts were in the range of about $10 million dollars. [2] (Table 3‑1)  So yes, $10 million for your life.

This is just a simple approximation today.  I’m sure an insurance firm has far more detailed assessments of human life, maybe even with variation by geographic location.  Maybe a person on the East Coast of the USA is worth more than someone on the West Coast.  I don’t know, I’m not an insurance actuarial.  And that shows one of the hardest parts of risk analysis:  accurate data is scarce and more precious than a human.  But for our argument, let’s assume a single human costs $10 million.  Life can be expensive.

4.0 The Probability of Disaster

Now that we know the cost of disaster, what are the odds?  This can be the hardest question to answer.  We frequently pay hundreds of dollars for accurate data sets.  I was not willing to pay that for a free article; so I limited my research to free resources.

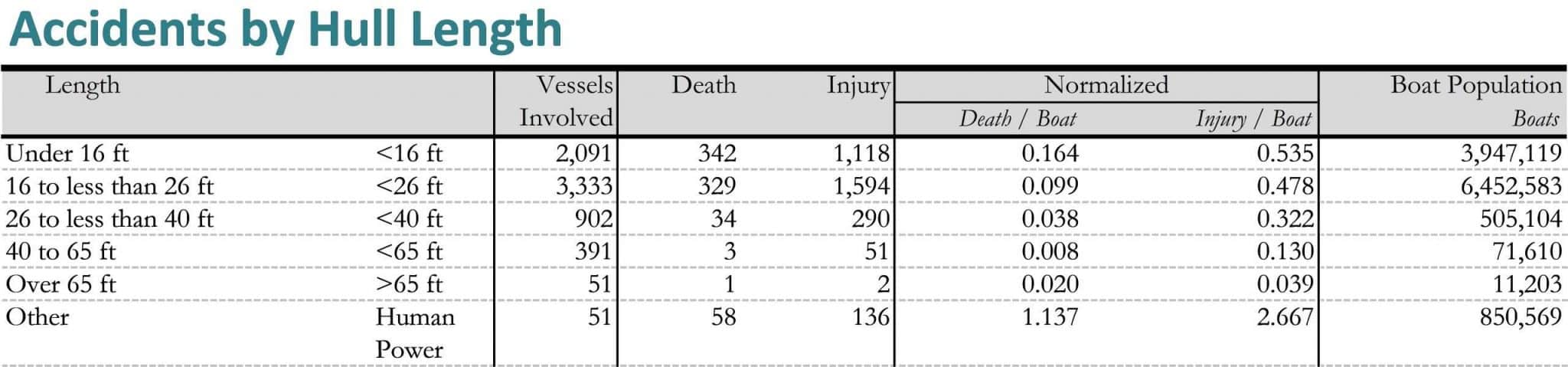
One great resource was the USCG annual boating safety report. [3]  This gave data on the total number of deaths and injuries, grouped by boat type. (Figure 4‑1)  But what do we compare these accidents against to get a probability?  Common options would be number of boats, total people on the water, or total time spent on the water.  Makes sense, the more time you spend on the water, the more chances you have to get in an accident.  But I’m presenting this from the perspective of a boat manufacturer.  The manufacturer only controls the boat.  Once we sell the boat, we don’t have any control over where the boat gets used, how often, or who uses it.  So I’m normalizing all accidents by the number of boats in that category.  This compares accidents against the one thing a manufacturer can control:  the boat.

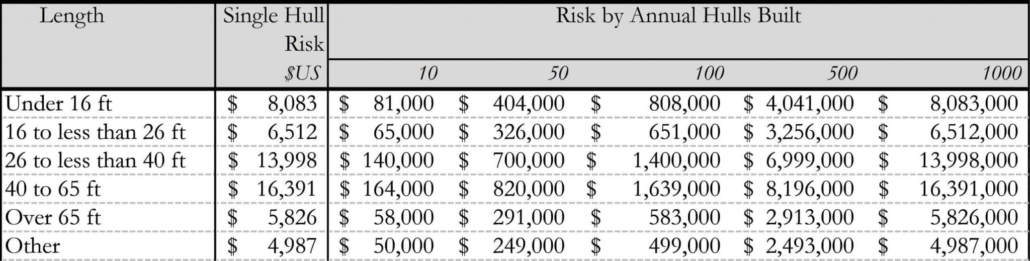
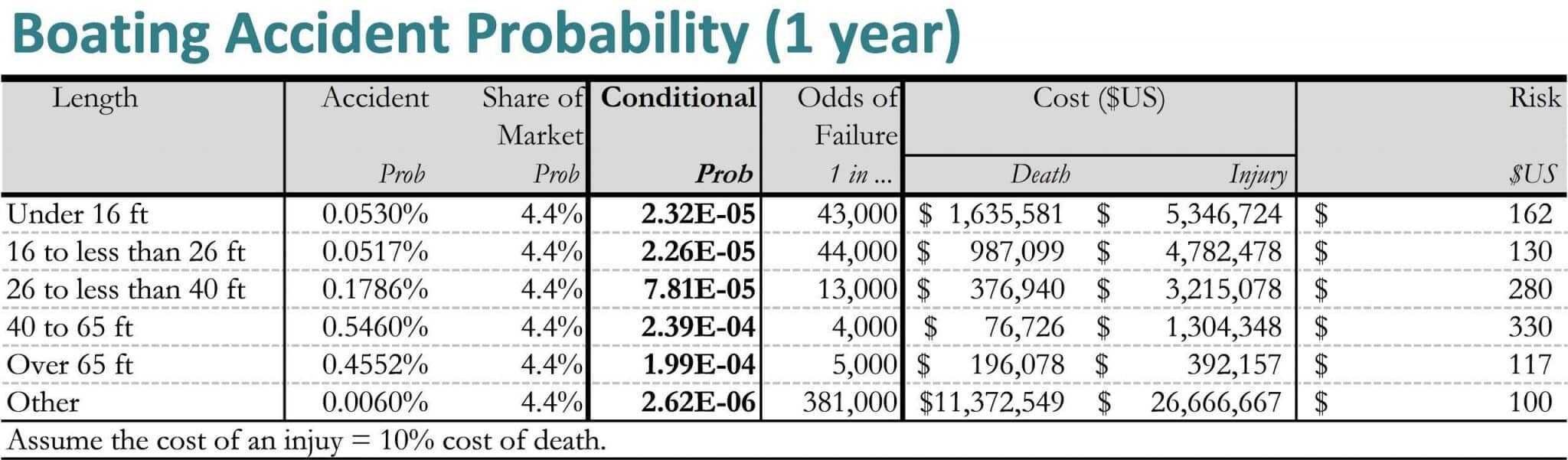
Great.  Now by comparing the number of boating accidents against total number of boats, we have the probability of an accident for each boat category. (Table 4‑1 and Table 4‑2)  But that doesn’t tell the whole story.  This probability includes all the boats currently on the market.  If a boating accident occurs, we also need the chances that the accident applies to one of the new boats that we just added.  This is called the conditional probability:  the combined chances of two bad things happening together. (Table 4‑2)

This gives a very low conditional probability, with odds in the range of 1:40,000, which is pretty good.  Not as safe as a nuclear reactor, but still fairly safe.  Thanks to the USCG data, we know the average number of deaths and injuries per boating accident.  Multiply that cost by the probability of failure, and we have the average risk.

5.0 The Risk of Building Boats

When I first saw that risk, it seemed too low.  Why would anyone pay to engineer a yacht if the risk was only a few hundred dollars?  Then I remembered where I got my data.  This was all based on the accidents from only a single year.  Manufacturers don’t sell a boat and then snatch it back after a year.  When you build and sell a boat, you accept the risk and potential lawsuits during the entire lifetime of that boat.  That risk that we saw in Table 4‑2 occurs every year.  We need to extrapolate to the total risk accumulated over the entire lifespan of the boat. (Table 5‑1)

Suddenly, the picture gets less rosy.  The risk starts to add up.  Remember, this is the financial risk for every boat you produce.  A risk that keeps growing as you produce more boats.  Now, consider a manufacturer that produces several hulls in a year.  That risk escalates into downright terrifying. (Table 5‑2)  Even the lowest category of boats under 16 ft.  They accumulate risk at $81,000 / year.  Compare that risk against the cost of engineering.  If the engineer charged $40,000 to create a safe design for those 10 boats, you still come out ahead, because it reduces the risk.

At this point I need to mention that I took several shortcuts in my analysis.  Somewhere a mathematician is yelling at their computer in frustration.  This style of presentation makes for snappy dialogue and compelling arguments.  But it hides the understanding behind the numbers.  In fairness, I produced a separate video pointing out all the detractors of this analysis.  For now, I accept that my findings have room for debate.  But my central point still stands.  The cost of engineering seems high.  The cost of failure is even higher. 

6.0 How Engineering Helps

Engineers are primarily there to guard you against disaster.  That is the value behind engineering.  This shows up in a few practical benefits:

1. Engineering creates the documentation to prove safety, and it is your best defense against a lawsuit.
2. In many cases, the engineer accepts responsibility for the design of the boat, shifting much of the legal liability away from you.  (I suspect attorneys would still try to sue you though.)

Beyond the business end, there is another reason in favor of engineering:  it simply makes the ship safer.  Every manufacturer I talk to always wants to build good quality, safe boats.  Engineers help to refine that idea.  When you ask “what is needed for safety?,” engineers find the answer. 

How much is that safety worth to you?  This risk analysis gives a good indication.  It also shows that safety is not just a comforting idea.  Safety adds real, quantifiable value to your product and business.  Engineers create safety.

7.0 References